Elo

Copy

• Copy for LLM

  Copy page as Markdown for LLMs
• View as Markdown

  Open this page as Markdown
• Open in ChatGPT

  Get insights from ChatGPT
• Open in Claude

  Get insights from Claude
• Connect to Cursor

  Install MCP server on Cursor
• Connect to VS Code

  Install MCP server on VS Code

The Elo rating system was originally developed to rank chess players. It has since been adapted and widely used to evaluate computer generated content based on pairwise comparisons [1, 2]. For instance, Elo scores have been used in the CLIC compression challenge to decide the ranking of image compression methods based on pairwise comparisons of images.

Underlying Elo scores is a probabilistic model of outcomes of pairwise comparisons. For competing methods $A$ and $B$ with Elo scores $E_A$ and $E_B$, the probability that $A$ is preferred over $B$ is assumed to be:

Here, we use the notation "$A>B$" to denote that $A$ was preferred over $B$ in a single pairwise comparison.

The standard algorithm for computing Elo scores is noisy and highly dependent on the order of ratings. Many research papers therefore report Elo scores averaged over thousands of random permutations of the data. Our platform instead implements a robust Bayesian inference algorithm for estimating Elo scores, which allows us to provide efficient live updates of Elo scores, along with uncertainty estimates. The scores are available on our platform in the results section of pairwise experiments.

Vanilla Elo scores

Let $Y_{AB}\in \{0,1\}$ represent the outcome of a pairwise comparison. For example, this could be the result of presenting two images to a human rater. If the image generated by method $A$ was preferred, $A>B$, we set $Y_{AB}=1$. If method $B$ was preferred, we set $Y_{AB}=0$. The basic update rule for vanilla Elo scores is as follows:

$$\begin{array}{l}{E}_A^{t+1}\leftarrow E_A^t+K\cdot (Y_{AB}-\text{Pr}(A>B\mid E_A^t,E_B^t))\\ E_B^{t+1}\leftarrow E_B^t+K\cdot (Y_{AB}-\text{Pr}(A>B\mid E_A^t,E_B^t))\end{array}$$

This update rule can be viewed as a stochastic gradient step on the log-likelihood of Elo scores,

where the dataset consists of triplets $(A,B,y)$ and $K$ is the step width.

Due to the lower reliability of vanilla Elo scores, they are enabled on our platform only on request. We use $K=30$ and initialize Elo scores at $2000$, following previous applications of Elo to the evaluation of images [1]. For ties, we set $Y_{AB}=0.5$. Vanilla Elo scores are updated once per pairwise comparison, which are processed in batches after a session completes.

Bayesian Elo scores

The probabilistic model underlying the Elo rating system is equivalent to the Bradley-Terry model [3]:

where the relationship between $S_A$ and Elo scores is

Note that the probabilities do not change if we add a constant $c$ to the Elo scores, or equivalently if we multiply the skill ratings $S_A$ by a constant factor.

Many methods for estimating the Bradley-Terry model have been proposed. Hunter [4], for example, proposed the MM algorithm corresponding to the update

where $w_A$ is the number of times method $A$ won against any other method, and $n_{AB}$ is the number of times $A$ was compared to $B$. Under a mild but technical condition, this algorithm is guaranteed to converge to the maximum likelihood estimate of the Bradley-Terry model [4].

Caron & Doucet [5] identified the above update as an expectation maximization (EM) algorithm. They further proposed placing a Gamma prior on the skill ratings $S_A$ with shape parameter $a$ and rate parameter $b$, leading to the following modified update rule:

Instead of EM updates, we perform mean-field variational inference updates [6], which are nearly identical:

This update rule is used when computing the scores "Elo (Bayesian)" on our platform. We use $a=0.1$, $b=0.1$, and $c=2000$ so that in the absence of any data, $S_A=1$ and $E_A=2000$. These parameters correspond to the prior distribution over Elo scores visualized below.

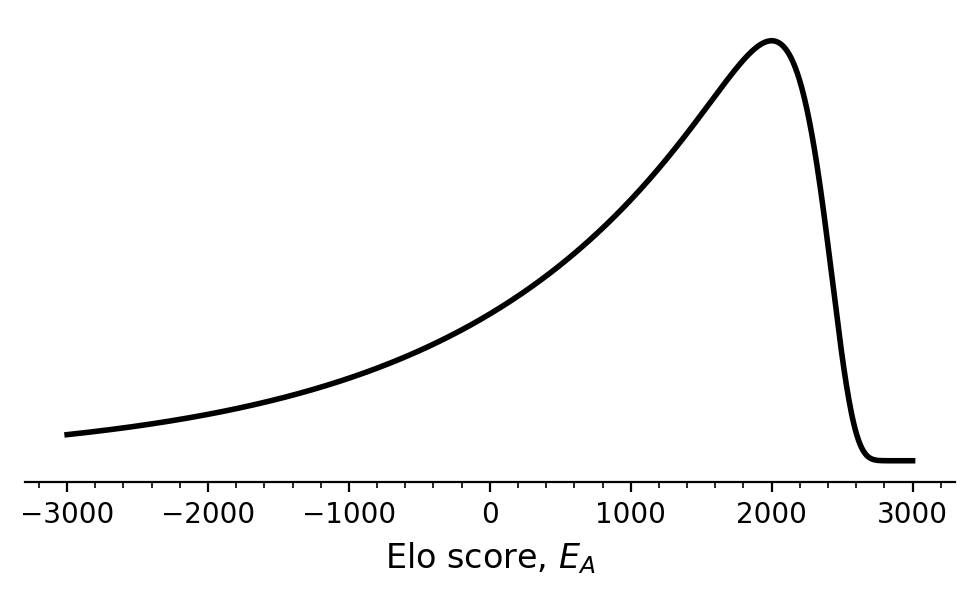
Unlike for vanilla Elo scores, we apply the update iteratively for up to 2 steps per pairwise comparison after every session that completes. Each step takes into account the entirety of the available data and updates all Elo scores.

Uncertainty estimates

The mean-field updates can be written as follows:

$$\begin{array}{l}{a}_A^{t+1}\leftarrow a+w_A\\ b_A^{t+1}\leftarrow b+\sum _{j:j\ne i}\frac{n_{ij}}{\frac{a_i^t}{b_i^t}+\frac{a_i^t}{b_j^t}}\end{array}$$

Here, $a_A$ and $b_A$ are the parameters of a Gamma distribution over the skill rating $S_A$. The expected value of $S_A$ under this distribution is $a_A/b_A$, which corresponds to our update rule above. Using this Gamma distribution, we compute 95% confidence intervals based on the 2.5th and 97.5th percentile.

References

[1] Mentzer et al. (2020). High-Fidelity Generative Image Compression.
[2] Askell et al. (2021). A General Language Assistant as a Laboratory for Alignment.
[3] Bradley, Terry, and Milton (1952). Rank Analysis of Incomplete Block Designs.
[4] Hunter (2004). MM algorithms for generalized Bradley–Terry models.
[5] Caron and Doucet (2010). Efficient Bayesian Inference for Generalized Bradley-Terry Models.
[6] Wainwright and Jordan (2008). Graphical Models, Exponential Families, and Variational Inference.